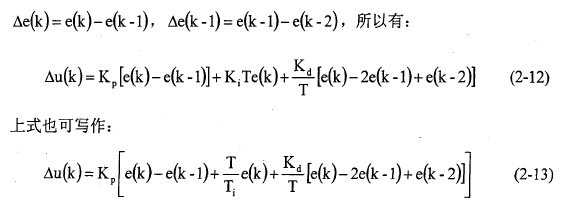智能控制系统之PID控制

PID控制方法是经典控制算法中的典型代表,与模糊控制结合,能够更好的发挥其优势。PD控制是**早发展起来的控制策略之一,具有鲁棒性好、可靠性高和结构简单的特点,适用面很广。PID控制器及其改进型是在工业过程控制中**常见的控制器。据统计,工业控制的控制器中Pro类占有90%以上。然而实际被控对象或过程往往难以建立精确的数学模型,具有非线性、时变不确定性,使用常规的PD控制算法不能得到理想的控制效果。智能控制理论的发展和计算机技术为解决复杂动态不确定系统的控制提供了新途径,也为PID的改进开辟了新空间。

IP功控制的发展

Pro的发展过程,实质上是参数自适应和参数整定方法的研究过程。[,91PID参数整定方法shou先由Ziegler和Nichols提出,之后许多技术被用于PID控制器的手动和自动整定。PD参数整定方法有多种划分方式。按发展阶段,划分为常规PID参数整定方法和智能PD参数整定方法;按控制量形式的组合,划分为非线性PID参数整定方法和线性PID参数整定方法,前者用于由非线性跟踪微分器和非线性组合方式生成的非线性PID控制器,后者用于经典PID调节器;按被控对象的多少`,划分为多变量Pro参数整定方法和单变量PD参数整定方法,前者是**近研究的难点及热点,后者囊括了现有的大多数整定方法。

智能PD参数整定方法包括基于规则的自整定方法和基于模型的自整定方法。基于模型的自整定方法是通过频率响应实验、参数估计及暂态响应实验来获取过程模型。基于规则的自整定方法的整定是基于类似有经验操作者手动整定的规则,不用获得过程实验模型。与基于模型的自整定方法一样,基于规则的自整定方法使用负载干扰、暂态响应或设定值改变等信息,对被控过程的特性观测。若被控量与设定值不符,则控制器参数进行基于规则整定。一般通过对响应特性进行量化,来获得一个基于规则的自整定过程。通常使用的量是描述控制回路响应速度的时间常数和振荡频率,以及用来描述控制系统稳定性的超调量和衰减比。获得决定不同控制器参数的相应规则应该增加或减少相对比较容易,但确定增减的量困难比较大。因此,连续自适应控制一般使用基于规则的整定方法。设定值变化的控制通常使用基于模型的整定方法,而在处理负载干扰和处理设定值变化的对象时基于规则的整定方法采用的处理方式相同。

从目前PD参数整定方法的研究和应用现状来看,今后的发展过程中研究和实践的重点和发展方向主要体现在以下几个方面:

(l)对于单输入单输出被控对象,需要进一步研究PID参数整定方法,针对不稳定被控过程或对象存在较大干扰的情况,增强在初始化和鲁棒性等方面的性能,尽量使用的操作简单且过程信息少,就可以很好的完成整定。

(2)对于多输入多输出被控对象,需要对多变量PD参数整定方法研究,针对多变量过程的显著藕合关系,使分散继电反馈方法进一步完善,使用到的先验信息量尽可能减少,易于在线整定。

(3)有待进一步研究智能PD控制方法和应用,将增益计划设定和自适应、自整定二者有机结合,使其增加自动诊断功能;对原有工控制器设计思想及整定方法进行改进,结合**经验知识、直觉推理逻辑等**系统思想和方法;为进一步提高控制系统性能,将PD控制、模糊控制和预测控制交叉应用。以上都是智能控制发展很有前途的*域。

ZP功控制的原理

PD控制器是将偏差的比例P、积分I、微分D线性并联组合的控制器[20]。

其数学模型可以用下式表示:

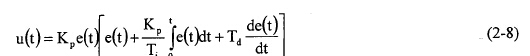
其中:e(t)—控制器的输入,是被控对象输出量和设定目标量的偏差信号

Ti—控制器的积分时间

KP—控制器的比例系数

Td—控制器的微分时间

u(t)—控制器的输出

式(2一8)表明比例、积分、微分三个校正环节构成了PID控制器的数学模型。

(l)t匕例环节。

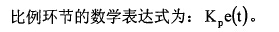
从数学表达式可知,积分环节的调节作用与偏差的积分成正比。不管存在偏差的大小,控制作用都会随时间的增加而不断增大。只有当偏差e(t)为o时,积分常数才为O,这时该部分不具有控制作用。可见,积分环节的作用是将系统的稳态误差消除。积分环节的作用受积分时间工的影响很大。当工较小时,积分有较强的作用,则系统过渡过程中有可能产生的超调较大,但只需较短的时间就可消除偏差;当工较大时,积分有较弱的作用,则系统过渡过程中不易产生超调,但是需要较长的时间消除偏差。因此,调节过程的初期,积分应当弱一些,甚**可以取零,之后应增强积分作用,有利于消除稳态误差。

(3)微分环节